Figure 1.
Quasi-static valence bond solid on an anisotropic triangular lattice, as suggested for κ-(BEDTTTF)2Cu2(CN)3. The spin singlets indicated in blue preferably form along the (b±c)-directions; domain walls between the valence bond patterns indicated in red. Local valence bond defects can occur at various kinds of grain boundaries; a local spin 1 2 can also be caused by the breaking of a singlet bond probably due to an anion layer vacancy, emphasized by the red circle.
Most solids with localized magnetic moments exhibit some sort of magnetic order at low temperatures, depending on lattice symmetry and magnetic interaction strength. However, geometrical frustration, quantum entanglement and disorder may prevent long-range order of localized spins despite strong exchange interactions, resulting in a novel state of matter. k-(BEDT-TTF)2Cu2(CN)3 is considered the best approximation of this elusive quantum-spin-liquid state, but its ground-state properties remain puzzling. In order to elucidate the magnetic ground state we have developed a novel broad-band electron-spin resonance spectroscopy that covers the range from 0.5 to 50 GHz and extends down to millikelvin temperatures. This way the transition to a valence-bond-solid can be identified below 6 K. An impurity contribution becomes dominant when the intrinsic spins form singlets. Only probing the electrons directly manifests the pivotal role of defects for the low-energy properties of quantum-spin systems without magnetic order.
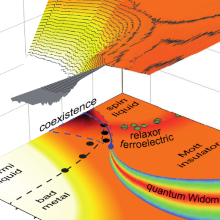
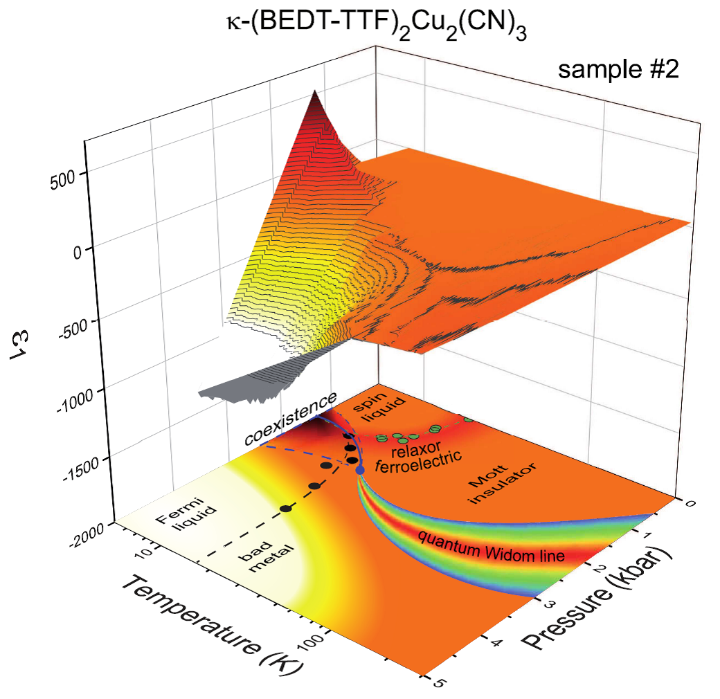
Figure 1 Contour plot of the dielectric permittivity e1(p,T) recorded at f = 380 kHz and the phase diagram of k-(BEDT-TTF)2Cu2(CN)3 as obtained by analysing e1(p; T) at 10 kHz. Most importantly, we observe a strong increase of e1 up to 500, centered around 1.8 kbar and below T = 20 K, close to the first-order Mott transition. We ascribe this to a coexistence phase hosting spatially separated metallic and insulating regions, as predicted by dynamical mean-field theory. For T > 16 K, the first-order insulator-to-metal transition becomes a gradual crossover which is indicated by the quantum Widom line.
The Coulomb repulsion among conduction electrons in solids hinders their motion and leads to a rise in resistivity. From the thermodynamic point of view, the transition between a correlated metal and a paramagnetic Mott insulator is supposed to be of first-order. Like for any first-order phase transition, theory predicts a parameter range where two phases coexist; in other words, a regime of electronic phase separation is expected near T = 0. However, for real electronic systems this remains unexplored experimentally as well as theoretically.
It is not possible to visualize the phase separation on a nanometer scale at very low temperatures by scatting probe techniques because the electronic correlations of the material have to be tuned via external pressure. Therefor we approach this issue by assessing the complex permittivity via dielectric spectroscopy, which provides vivid mapping of the Mott transition and deep insight into its microscopic nature. Our low-temperature experiments reveal a strong enhancement of the quasi-static dielectric constant e1 when correlations are tuned through the critical value by hydrostatic pressure or chemical substitution.
All experimental trends are captured by dynamical mean-field theory of the single-band Hubbard model supplemented by percolation theory. The description combines classical statistical percolation theory with quantum mechanical theory of the correlation driven transition between to electronic ground states Our findings suggest a similar ’dielectric catastrophe’ in many other correlated materials.
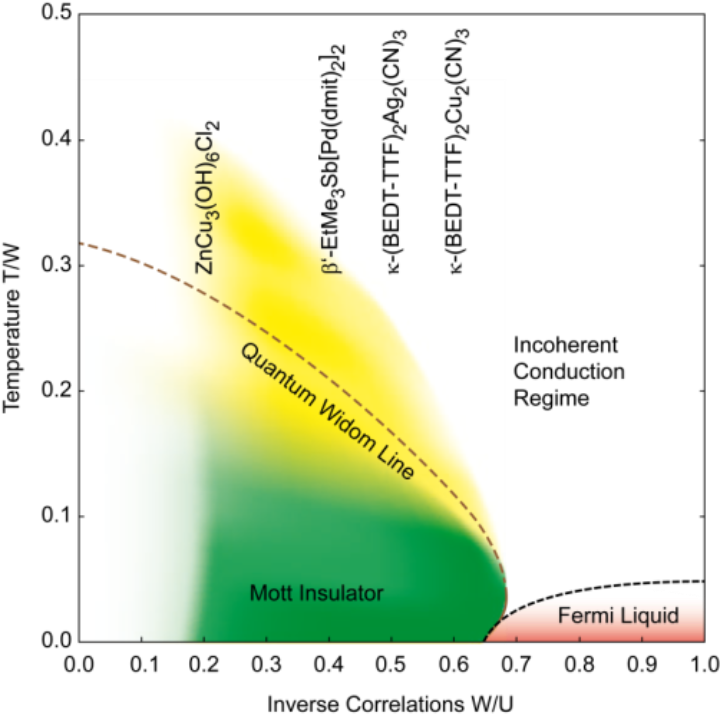
The physics of strongly correlated materials is at the forefront of research in condensed matter physics, boosted by the discovery of high-Tc cuprates. The relationship between correlations and unconventional superconductivity, quantum spin liquid behavior and other exotic states of matter has been intensively debated. While at the level of model theories one can introduce quantitative criteria for the degree of correlation, such as the ratios U/W or V/W, where U and V are the on- and inter-site Coulomb repulsion, respectively, and W is the single-particle bandwidth, in most materials the single-band Hubbard model is not applicable.
Organic conductors provide a perfect laboratory to study and tune the effects of electronic correlations. The related energy scales are about two orders of magnitude smaller than in transition-metal compounds, such as vanadium oxides or cuprates, for instance. Thus, the effects of charge and spin localization can be accessed at significantly lower temperatures (1 – 100 K) and the bandwidth can be tuned by comparably small applied pressures (0.01 – 10 GPa) , providing access to so far inaccessible regions in the phase diagram.
Our main research interest focuses on the quasi two-dimensional (BEDT-TTF)2X as well as on the quasi one-dimensional Fabre and Bechgaard salts, (TMTTF)2X and (TMTSF)2X. In these charge transfer salts electrons are donated from the organic molecules to the anions X generating partially-filled bands on the organic molecules. Since the occupied anion bands are typically more than 1 eV (8000 cm-1) lower in energy, these systems provide the ideal framework to study the physics of the single band Hubbard model. In particular, our current investigations focus on materials exhibiting diverse unconventional phenomena, including Mott insulators, quantum spin liquids, superconductors, bad metals, Fermi liquids and Luttinger liquids.
We employ optical spectroscopy to study the effects of electronic correlations, such as the opening of a gap in the absorption spectrum in the course of a metal-insulator transition, covering a frequency range from 10 – 47000 cm-1. Several optical cryostats and a pressure cell allow us to cover temperature, pressure and magnetic field ranges of 1.8 - 350 K, 0 - 2 GPa and 0 – 7 T, respectively. In addition, we provide dc transport facilities with essentially the same specifications, as well as electron spin resonance and SQUID magnetometry.
Most solids with localized magnetic moments exhibit some sort of magnetic order at low temperatures, depending on lattice symmetry and magnetic interaction strength. However, geometrical frustration, quantum entanglement and disorder may prevent long-range order of localized spins despite strong exchange interactions, resulting in a novel state of matter. k-(BEDT-TTF)2Cu2(CN)3 is considered the best approximation of this elusive quantum-spin-liquid state, but its ground-state properties remain puzzling. In order to elucidate the magnetic ground state we have developed a novel broad-band electron-spin resonance spectroscopy that covers the range from 0.5 to 50 GHz and extends down to millikelvin temperatures. This way the transition to a valence-bond-solid can be identified below 6 K. An impurity contribution becomes dominant when the intrinsic spins form singlets. Only probing the electrons directly manifests the pivotal role of defects for the low-energy properties of quantum-spin systems without magnetic order.
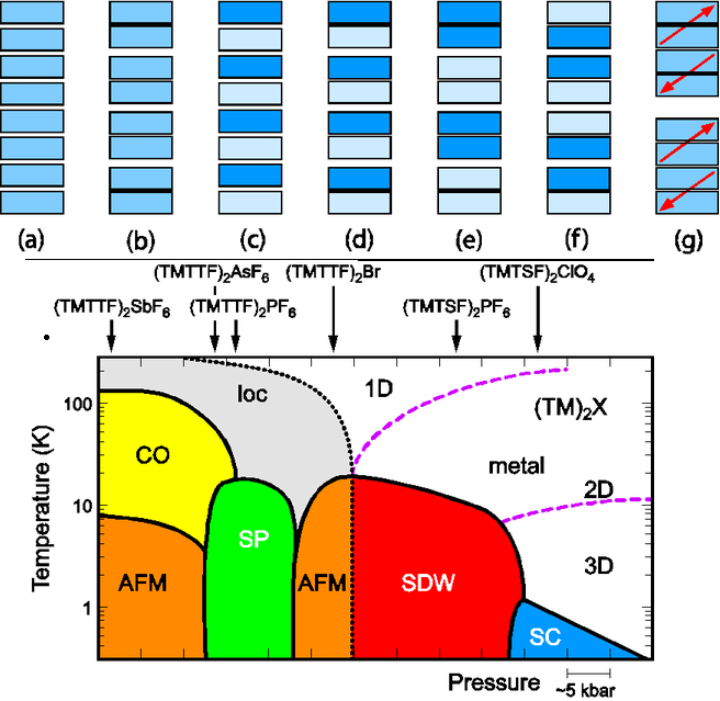
Low-dimensional organic conductors are model systems for investigating the physics in reduced dimensions. In the metallic state of a one-dimensional solid, Fermi-liquid theory breaks down, and spin and charge degrees of freedom become separated. But the metallic phase is not stable in one dimension: as the temperature is reduced, the electronic charges and spins tend to arrange themselves in an ordered fashion due to strong correlations.
The competition of the different interactions is responsible for which broken-symmetry ground state is eventually realized in a specific compound and which drives the system toward an insulating state. Here, we review the various ordering phenomena and how they can be identified by optic and magnetic measurements. While the final results might look very similar in the case of a charge density wave and a charge-ordered metal, for instance, the physical cause is completely different. When density waves form, a gap opens in the density of states at the Fermi energy due to nesting of the one-dimension Fermi surface sheets. When a one-dimensional metal becomes a charge-ordered Mott insulator, on the other hand, the short-range Coulomb repulsion localizes the charge on the lattice sites and even causes certain charge patterns. There are interesting similarities and conceptional differences of these phenomena. Particular emphasis of our research is on collective phenomena that are inherently present as soon as ordering breaks the symmetry of the system.
We explore the experimental aspects of electronic ferroelectricity and related electrodynamics in the one-dimensional (TMTTF)2X and TTF-CA, and in the most prominent phases of two-dimensional (BEDT-TTF)2X molecular charge-transfer solids.
By now it is well understood that electronic ferroelectricity is established in (TMTTF)2X and TTF-CA, as well as in α-(BEDT-TTF)2I3 and the relaxed state of θ-(BEDT-TTF)2RbZn(SCN)4. Macroscopic electric polarization arises due to valence instability in TTF-CA and long-range charge order in the others; and is stabilized by a subtle interplay of Coulomb forces and structural changes. The charge disproportionation was evidenced by a variety of experimental techniques including NMR, x-ray and neutron diffraction, Raman and infrared vibrational spectroscopy and optical second harmonic generation; they probe the local order as well as the global symmetry.
Remarkably, even when non-equivalent bonds are already present in the native structure, additional structural changes set in and enhance the breaking the inversion symmetry. Type and magnitude of changes differ for these compounds ranging from dimerization in TTF-CA and changes of dihedral angles in α-(BEDT-TTF)2I3, changes of dihedral angles accompanied by doubling of the unit cell in θ-(BEDT-TTF)2RbZn(SCN)4 to an uniform anion shift as a whole in the (TMTTF) salts. The role of cation-anion hydrogen bond interactions have been also suggested for (TMTTF)2X and α-(BEDT-TTF)2I3. Taken together experimental data and current theoretical approaches, there are clear indications that the stabilization of electronic ferroelectricity takes place by a cooperative process between Coulomb interactions and coupled molecular cation-anion subsystems.
The electrodynamic properties demonstrating the ferroelectric nature of the charge-ordered state include: a Curie-like peak of the dielectric constant and its characteristic dispersion, strong non-linear effects, switching, polarization hysteresis and ultra-fast dynamics. Polarization hysteresis, commonly taken as a basic piece of evidence for ferroelectricity has only been observed in TTF-CA. The missing evidence in the other systems may be due to either relatively high conductivity or to a low breakdown field; certainly more efforts are needed to clarify this issue.
Optical nonlinearity and ultra-fast photo-response observed in TTF-CA, and in α-(BEDT-TTF)2I3 and θ-(BEDT-TTF)2RbZn(SCN)4 strongly support an intrinsic electronic origin of the ferroelectricity. Effects include the light-induced melting of the charge-ordered state and creation of metallic domains within extremely short times at the level of pico- to femtoseconds and decay back to the original state. A quantitative difference observed in photo-induced dynamics among these systems can be correlated with different structural changes involved in the formation of the ferroelectric state. On the other hand, dc electric field-induced effects such as negative differential resistance and switching happen within much longer, i.e. millisecond time scales and thus can hardly be explained by melting. One of the plausible mechanisms involves the domain wall dynamics; this issue remains to be explored further. The formation of ferroelectric domains was visualized by electro-reflectance and optical second harmonic generation interferometry in TTF-CA and α-(BEDTTTF)2I3; their presence was invoked in interpretation of the dielectric response at lower temperatures, away from the charge-ordering phase transition in (TMTTF)2X, TTF-CA and α-(BEDT-TTF)2I3.
The dielectric response features a Curie peak with negligible dispersion at the charge ordering and neutral-to-ionic phase transition temperature and a characteristic response at lower temperatures. Pre-transitional effects are also observed in α-(BEDT-TTF)2I3 and relaxed state of θ-(BEDT-TTF)2RbZn(SCN)4 up to room temperatures. Anomalous features of the dielectric response indicate the critical role of random potential arising due to internal heterogeneity. It may influence the scale at which charge order develops thus, for example, affecting the formation of a Curie peak at the phase transition, and even resulting in relaxor ferroelectricity in nominally pure single crystals, as observed for (TMTTF)2X and TTF-CA. Importantly, for the best single crystals, estimates of charge disproportionation deduced from the Curie constant strongly deviate from well-established values for (TMTTF)2X and TTF-CA, while they are close to them for α-(BEDT-TTF)2I3 and θ-(BEDT-TTF)2RbZn(SCN)4. These findings are intriguing and call for further considerations.
Finally, we have taken a look at the electrodynamical properties of two most challenging materials κ-(BEDT-TTF)2Cu[N(CN)2]Cl and κ-(BEDT-TTF)2Cu2(CN)3 suggested as candidates for a molecular multiferroic and quantum spin liquid, respectively. These systems display an anomalous dielectric response in the absence of structural changes and with no evidence for charge disproportionation within the dimers. A polarization hysteresis and bistable resistance are also reported for κ-(BEDT-TTF)2Cu[N(CN)2]Cl. Advanced experimental probes and theoretical approaches are required to achieve a very much needed breakthrough in understanding of these phenomena.
- Pustogow, R. Rösslhuber, Y. Tan, E. Uykur, M. Wenzel, A. Böhme, A. Löhle, R. Hübner, Y. Saito, A. Kawamoto, J. A. Schlueter, V. Dobrosavljević, and M. Dressel
Low-Temperature Dielectric Anomalies at the Mott Insulator-Metal Transition
arXiv:1907.04437 - Rösslhuber, A. Pustogow, E. Uykur, A. Böhme, A. Löhle, R. Hübner, J. Schlueter, Y. Tan, V. Dobrosavljević, and M. Dressel
Phase coexistence at the first-order Mott-transition revealed by pressure-dependent dielectric spectroscopy of κ-(BEDT-TTF)2Cu2(CN)3
arXiv:1911.12273 - Saito, R. Rösslhuber, A. Löhle, M. Sanz Alonso, M. Wenzel, A. Kawamoto, A. Pustogow, and M. Dressel
Bandwidth-tuning from insulating Mott quantum spin liquid to Fermi liquid via chemical substitution in κ-[(BEDT-TTF)1-x(BEDT-STF)x]2Cu2(CN)3
arXiv:1911.06766 - A. Pustogow, M. Bories, A. Löhle, R. Rösslhuber, E. Zhukova, B. Gorshunov, S. Tomić, J.A. Schlueter, R. Hübner, T. Hiramatsu, Y. Yoshida, G. Saito, R. Kato, T.-H. Lee, V. Dobrosavljević, S. Fratini, and M. Dressel
Quantum Spin Liquids Unveil the Genuine Mott State
arXiv:1710.07241 (2017) - M. Dressel and T. Peterseim
Infrared Investigations of the Neutral-Ionic Phase Transition in TTF-CA and its Dynamics
Crystals 7, 17 (2017) - M. Dressel, P. Lazic, A. Pustogow, E. Zhukova, B. Gorshunov, J.A. Schlueter, O. Milat, B. Gumhalter, and S. Tomic
Lattice vibrations of the charge-transfer salt κ−(BEDT-TTF)2Cu2(CN)3: Comprehensive explanation of the electrodynamic response in a spin-liquid compound
Physical Review B 93, 081201 (2016) - T. Peterseim, P. Haremski and M. Dressel
Random-Walk Annihilation Process of Photo-Induced Neutral-Ionic Domain Walls in TTF-CA
Europhysics Letters (EPL) 109, 67003 (2015) - S. Tomić and M. Dressel
Ferroelectricity in Molecular Solids: A Review of Electrodynamic Properties
Reports on Progress in Physics 78, 096501 (2015) - K. Sedlmeier, S. Elsässer, D. Neubauer, R. Beyer, D. Wu, T. Ivek, S. Tomić, J. A. Schlueter, and M. Dressel
Absence of charge order in the dimerized κ-phase BEDT-TTF salts
Physical Review B 86, 245103 (2012) - M. Dressel, M. Dumm, T. Knoblauch, B. Köhler, B. Salameh, and S. Yasin
Charge Order Breaks Magnetic Symmetry in Molecular Quantum Spin Chains
Advances in Condensed Matter Physics 2012, 398721 (2012) - M. Dressel
Quantum criticality in organic conductors? Fermi-liquid versus non-Fermi-liquid behavior
J. Phys. Condens. Matter 23, 293201 (2011) - C. Schlegel, J. van Slageren, A. Manoli, E.K. Brechin, M. Dressel
Direct Observation of Quantum Coherence in Single-Molecule Magnets
Phys. Rev. Lett. 101, 147203 (2008) - J. Merino, M. Dumm, N. Drichko, M. Dressel, and R. H. McKenzie
Quasiparticles at the verge of localization near the Mott metal-insulator transition in a two-dimensional material
Physical Review Letters 100, 086404 (2008) - M. Dressel
Ordering Phenomena in Quasi One-Dimensional Organic Conductors
Naturwissenschaften 94, 527 (2007) - M. Dressel and N. Drichko
Optical Properties of Two-Dimensional Organic Conductors: Signatures of Charge Ordering and Correlation Effects
Chemical Reviews 104, 5689 (2004) - M. Dressel
Spin-charge separation in quasi one-dimensional organic conductors
Naturwissenschaften 90, 337 (2003)