Quantum Electric Dipoles

We want to investigate quantum electric dipoles realized by H₂O molecules confined to nanocages of crystals. Since the isolated water molecules do not form hydrogen bonds, they constitute an almost ideal model of a quantum electric dipole lattice. At high temperatures the water molecules rotate within the cavities. At low temperatures, we dis­covered tunneling behavior within the nanocage that smears out the positions of the protons into a pair of corrugated rings; the tunnel splitting is estimated to be around 1 meV. We study the energy levels of nano-confined water molecules in several dielectric frameworks, such as cordierite, analcime, natro­lite, dioptase, which exhibit differ­ent cage geome­tries, and bikitaite with elongated channels with one-dimensional H₂O chains. In particular, we use broad-band optical spectro­scopy in order to investigate the rotational and vibra­tional modes of light and heavy water. This provides information about the interaction with the cage walls, the doping atoms in the structure and their vibrations. Even the nuclear-spin isomers, para and ortho-water, can be addressed by our spectroscopic methods. Quantum-mechanical simulations within the Density Functional Theory approach, as well as Molecular Dynamics are utilized to model all systems mentioned above and develop a deep understanding of how quantum tunneling and fluctuations affect the properties and behavior of the confined electric dipoles.

In addition we address the dipolar interaction between the H₂O molecules that eventually leads to more or less long-range order and the occurrence of an incipient ferroelectric state of water in beryl, for instance. We explore how the anisotropic dipole-dipole coupling forms a three-dimensional cooperative many-body state from the delocalized H₂O molecules. Here, low-frequency optical and dielectric investigations at low temperatures are the superior methods for the interaction strength of approximately 10 meV. Starting with the prototype beryl, the length of dipolar chains in the c-axis channels can be modified by varying the filling. By applying pressure, we can increase the dipolar coupling. The anisotropic interactions are reflected in the polari­za­tion-dependent optical and dielectric response. We also study the influence of an external electric field and the possibility of domain wall motion. We go beyond beryl with its particular triangular ab-lattice and investigate other nano-porous crystals, and, consequently, altered couplings between the confined H₂O molecules. This modifies the strength of the dipolar interaction and cause anisotropy within the ab-plane. When the coupling in c-direction is dominant, chains of electric dipoles are realized with the possibility to study their excitation spectrum; if this coupling becomes inferior, the system may be treated as two-dimen­sional with a geometry imposed by the crystal lattice of the dielectric framework. The interplay of quantum tunneling, fluctuation, and frustration among the coupled electric dipoles could finally provide the possibility to realize a quantum electric dipole liquid and glasses.

Although water molecules carry a large electric dipole moment, neither liquid nor solid water reveal dipolar order, because the dipole-dipole-interaction is suppressed by the short-range hydrogen bonds. In liquid water, the hydrogen bonds lead to various clustered structures. Nevertheless, there are attempts to realize ordering of H₂O molecular dipoles in cases, when water molecules or groups of molecules are confined by some external framework or located within nano- or micro-sized pores. Numerous computer simulations demonstrate possibilities of ferroelectric or antiferroelectric orderings of H₂O molecules within carbon nanotubes, fullerenes or spread over two-dimensional surfaces, for instance. The activity is stimulated by the fact that this kind of confined-water ferroelectricity is considered to play a significant role in various processes in nature, including living organisms. Until now, however, no clear and incontrovertible evidences have been obtained for any kind of H₂O dipoles ordered state.

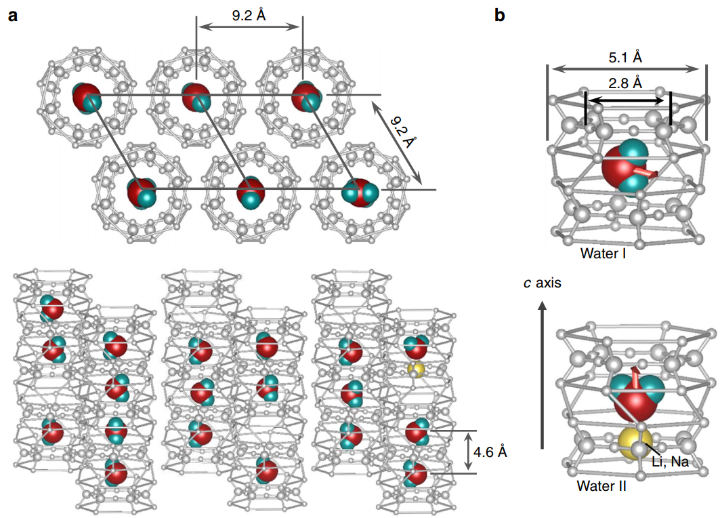
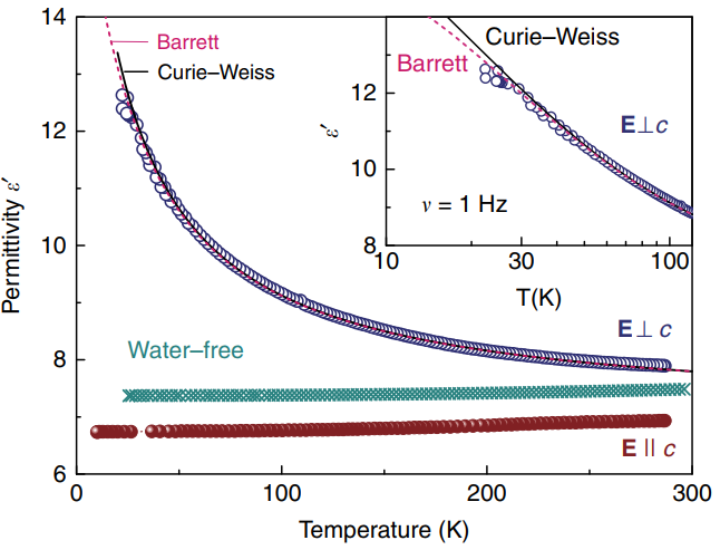
We have studied the dielectric response of a system of water molecules localized within structural channels formed by ions of the beryl crystal lattice. The distance between the pores that form the channels and host water molecules is large enough (5 Å and 10 Å along the two main crystallographic directions) to rule out hydrogen bonds but short enough to keep the long-range dipole-dipole coupling effective. By terahertz and radio-frequency spectroscopies, we have detected firm signatures of crystalline matrix. At terahertz frequencies, we detect an ordering within the subsystem of H₂O molecules in the ferroelectric soft mode whose dielectric contribution leads to the Curie-Weiss temperature dependence of the static dielectric constant. Below 10 K, we observe saturation of the dielectric constant and of the soft-mode parameters that indicate incipient ferroelectricity of the water molecules. We describe our results within the framework of a mean-field microscopic model that considers rotational and librational motions of interacting water molecular dipoles in a six-well potential.