Description
Our research revolves around light – matter interactions and in particular in the scattering of an incident light field. We perform spectroscopic measurements in the visible and focus in particular on polarization states. Most of our measurements consist in sending a known radiation on our samples and measure the so-called Mueller matrix. It provides a complete description of the optical response for a given energy and direction.
We work with large ensembles of oriented or disoriented nano scatterers, in particular metallic nano antennas arranged on a substrate. This allows designing meta-materials with a tuneable and controlled energy and the phase for an incident wavefront. We are also interested in systems of dense scatterers populations where the incoming polarized beam becomes randomly polarized. Time and space inhomogeneities alter the polarization of a light beam and multiple scattering events can produce a strong depolarization.
Samples thickness goes from a few nanometers to a few micrometers usually as a thin film. The spectroscopic ellipsometry approach allows determining the optical properties (refractive index, thickness) of the material.
Current Research Topics
- Active control of the optical properties of plasmonic structures through tailored disorder
- Dispersion engineering and meta-materials
- Light depolarization in strongly scattering environments
- Linear and nonlinear properties of metallic thin films close to the percolation threshold
- Optical characterization of biological materials
Selected Publications
A. Konzelmann, H. Charaya, B. Gompf, M. Dressel and A. Berrier
AIP Advances 8, 075012 (2018)
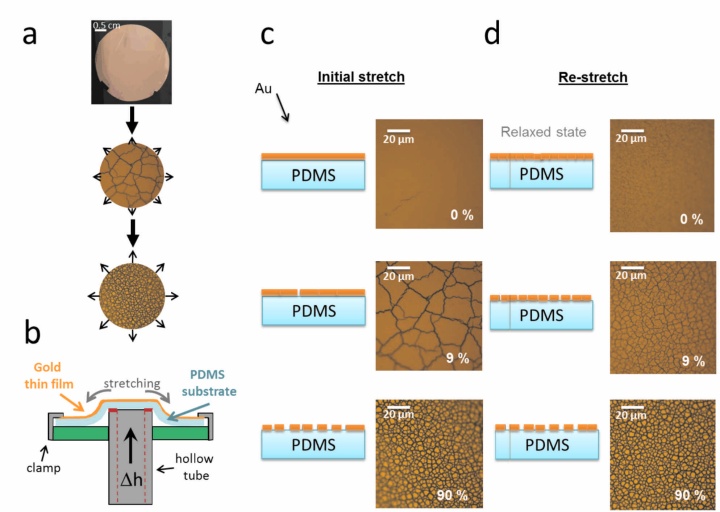
When crossing the percolation threshold the optical behavior of thin metal films dramatically change within a narrow range. Recording the optical properties in the vicinity of the percolation provides insight into the interplay of those contributions that determine the intensity of the second harmonic signal: the metallic islands and the dielectric gap between the islands. Here we demonstrate the active tuning of the linear and nonlinear optical properties of a thin gold film on a stretchable PDMS substrate. Ellipsometry was combined with nonlinear studies (second-harmonic generation) to describe the optical properties of thin gold films around the percolation.We monitor the metal-insulator transition, characterize the evolution of the permittivity of the layer, and explain the strength variations of the second harmonic generation with respect to the spectral difference between fundamental wavelength and plasmonic resonance, as well as the enhancement of the field in the dielectric gaps as a function of the particle-particle distance. A model reproduces the experimental observations by taking into account both effects at the fundamental and at the generated wavelengths.
M. Wang, B.Gompf, M. Dressel, N. Destouches and A. Berrier
Optical Materials Express 8 (6) 1515-1527 (2018)
Although chiroptical effects in plasmonics attract great interest, the nature of the observed circular dichroism (CD) is often not clearly discussed. Here we demonstrate how Mueller matrix ellipsometry can be used to identify the physical origin of different polarization mixing effects, such as true CD, anisotropy or dispersion. We apply the method to a complex design: large area arrays of curved silver nanoparticle rows, embedded in a high index waveguide, fabricated by laser-induced self-assembly. This sample presents both induced linear CD and true CD. The method is widely applicable to all artificial designs and reveals the complex origin of the optical properties.
Bruno Gompf, Maximilian Gill, Martin Dressel, and Audrey Berrier
JOSA A, 35, 301-308 (2017)
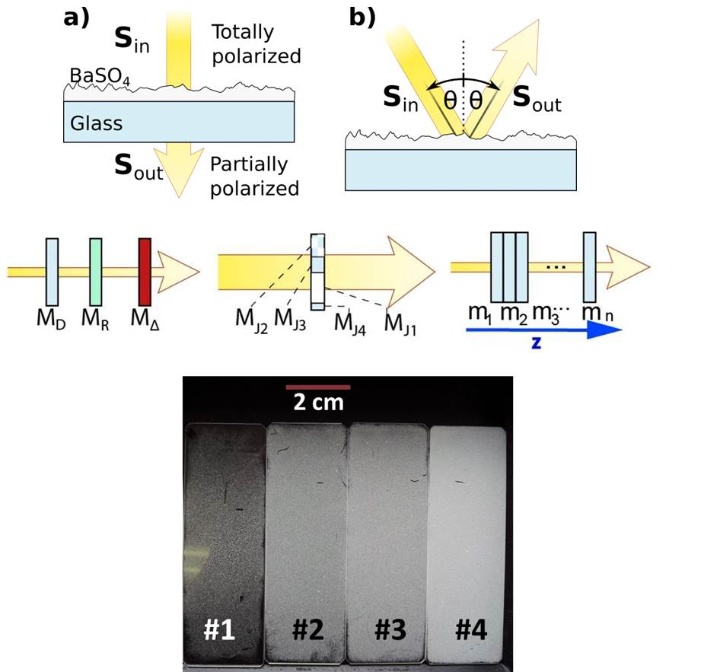
We describe a general method to disclose the information hidden in Mueller matrices experimentally obtained from depolarizing samples. Although spectroscopic Mueller-matrix ellipsometry allows for a model-free characterization of inhomogeneous samples, i.e., independently from any assumption on the sample structure, the interpretation of the obtained results is often challenging. The proposed method combines three different decomposition techniques applied to the measured Mueller matrices in transmission and reflection of granular thin films with different thicknesses and densities. We demonstrate that the comparative analysis of the respective differential-, product-, and sum-decomposition of the Mueller matrices, together with correlation effects and the visualization as a Poincaré sphere, reveals the particular underlying physical processes of depolarization. As an example, we apply this method on granular BaSO4 thin films. This method is general and can be applied to a wide variety of intrinsically inhomogeneous materials with applications in physics, industry, biology, or medicine.
The geometrical arrangement of metallic nanoparticles plays a crucial role on the optical response of nanoplasmonic samples due to particle-particle interactions. In this work, large-area, two-dimensional meta-glasses (random arrangements) and meta-crystals (periodic arrangements) made of identical metallic nanoparticles are investigated for three different particle densities of 5, 10, and 15 discs/μm2. A direct comparison between random and periodically ordered arrays is presented. The comparison clearly shows that the particle density has the largest influence on the extinction spectra for both periodic and random samples, and that for equal densities, the optical response away from diffraction effects is strikingly similar in both cases. The role of the radial density function and minimum particle distance is also determined. This study elucidates the role of the particle-particle interactions on the response of plasmonic nanoparticles and indicates how to control position and shape of the plasmonic resonance.
S. De Zuani, M. Rommel, R. Vogelgesang, J. Weis, B. Gompf, M. Dressel, and A. Berrier
Large-Area Two-Dimensional Plasmonic Meta-Glasses and Meta-Crystals: a Comparative Study
Plasmonics, 2016, 10.1007/s11468-016-0397-9
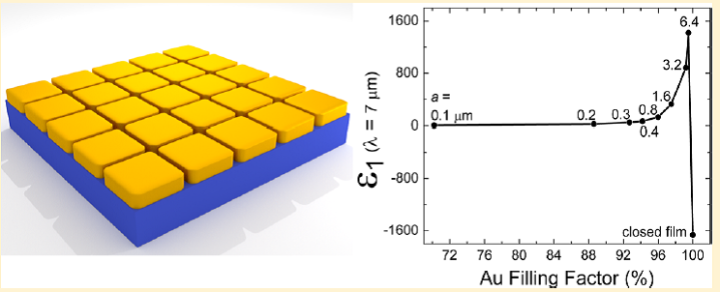
Metal−dielectric composites exhibit remarkable properties at the percolation threshold. A small variation of the filling factor can lead to a huge variation in the dc conductivity from an insulator-like to a metal-like behavior while the real part of the permittivity diverges. This behavior can, in principle, be described by percolation theories at low frequencies and by effective medium approximations at higher frequencies. These theories assume a random distribution of the metallic inclusions inside the insulating matrix. But what happens in ordered structures when the percolation is deliberately suppressed? Even though a simple, nanometer-wide scratch can deteriorate the dc conductivity of a thin metal film, can it influence the mirror-like reflectivity? To address this question, we perform a systematic ellipsometric investigation on nearly closed Au films interrupted only by a two-dimensional periodic mesh of 20 nm wide lines. These nanostructured films have metal filling factors close to unity, but exhibit no dc conductivity. In the infrared, they show an antireflective behavior that can be tuned through the mesh periodicity. Surprisingly, the optical response of these structures can be modeled quite well by simple effective medium approximations. Increasing the size of the squares leads to a tunable, diverging, real part of the permittivity: a maximum of the real part of the permittivity of 1420 is found for the largest investigated squares in this study.
S. De Zuani, M. Rommel, B. Gompf, A. Berrier, J. Weis, and M. Dressel
Suppressed Percolation in Nearly closed Gold Films
ACS Photonics 3, 1109 (2016)
The samples investigated in this study are 50nm thick gold wires made by electron beam lithography following the pattern corresponding to a Hilbert curve of order 9. They show an in-plane isotropic, metallic behavior while they have dielectric properties in the out-of-plane direction. The reflectance of these samples is almost flat in a wide spectral range and their optical properties can be tuned by acting on the wire thickness.
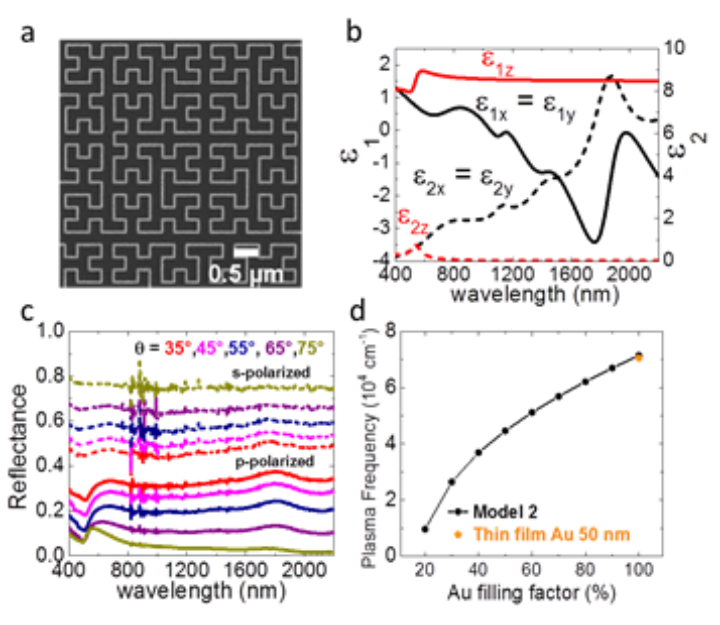
Ultra-thin metal films exhibit an isotropic nearly frequency independent optical behavior, which theoretically can be tuned by their thickness. In practice however, below a certain critical thickness, the so-called percolation threshold, they undergo a metal-to-insulator transition, where the dielectric properties diverges. One way to overcome this problem is to look for continues metal structures with a homogeneous, isotropic and frequency independent behavior. Self-similar structures are promising candidates as non-periodic, non-resonant structures exhibiting a homogeneous, isotropic and frequency-independent effective optical response. Hilbert fractal curves in particular are self-avoiding, continuous curves, proposed for the first time by David Hilbert in 1891 as a particular geometry of a family of curves introduced by Giuseppe Peano in 1890, known as “FASS-curves” (space-filling, self-avoiding, simple and self-similar). Our experiments show that high-order Hilbert nanostructures of fractal order N = 9 exhibit a nearly frequency independent reflectance and an in-plane isotropic optical response. The response can be simulated in the framework of a simple Bruggeman effective medium approximation (BEMA) model with a limited number of parameters. High-order Hilbert structures can be considered as a “transparent in-plane metal”, which dielectric function is modified by the filling factor f, hence creating a tunable conductive effective metal with tailorable plasma frequency and variable reflectance without going through an insulator-to-metal transition.
S. De Zuani, T. Reindl, M. Rommel, B. Gompf, A. Berrier, and M. Dressel
ACS Photonics 2, 1719 (2015).
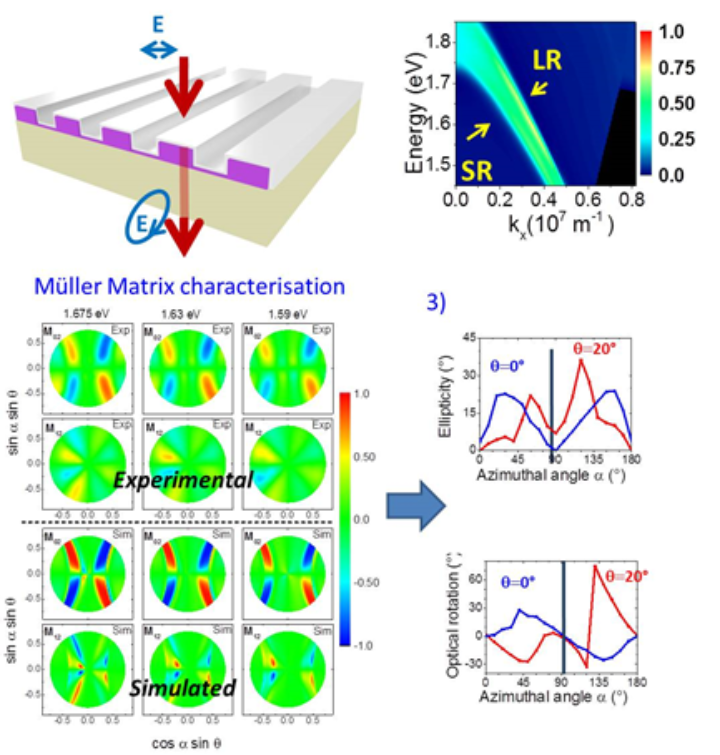
The samples, made of a thin silver layer evaporated onto MF2 one-dimensional gratings, are operating in transmission. It transforms a linearly polarized beam into circularly polarized light. The dispersion diagram is characterized by a large, dispersive passband. The Mueller matrices reveal the excited modes as a coupling between the short range (SR) and the long range (LR) surface plasmon polaritons across the thin silver layer. The measured Mueller matrix data are used to calculate both the ellipticity and the optical rotation of the meander sample.
The fascinating optical properties of metamaterials and metasurfaces are intrinsically wave-vector (k) dependent and spatial dispersion effects induce a complex optical response. We use Mueller matrix spectroscopic ellipsometry, providing both amplitude and phase information in the visible, is used in a large frequency and k-space range to characterize a plasmonic meander and assign the polarization effects to the microscopic plasmonic excitations of a metasurface. The measurement of Mueller matrices leads to a fundamental physical insight into the optical properties of the plasmonic meanders: the effect of closed-film resonant coupling is used for large polarization rotation and high transmission, and multiple optical functions are created within one compact design, which cannot be obtained by any natural crystal.
A. Berrier, B. Gompf, L. Fu, T. Weiss, H. Schweizer
Phys. Rev. B 89, 195434 (2014)
Contact

Bruno Gompf
Dr.Ellipsometry